ini dia lanjutan Pembahasan Soal Ujian Nasional SMA IPA 2010 Bagian 4
-
Diketahui kubus $ABCD.EFGH$. Nilai kosinus sudut antara $CH$ dan bidang $BDHF$ adalah…
A. $\frac 12$
B. $\frac 13\sqrt3$
C. $\frac 12\sqrt2$
D. $\frac 12\sqrt3$
E. $\sqrt3$
Jawab :
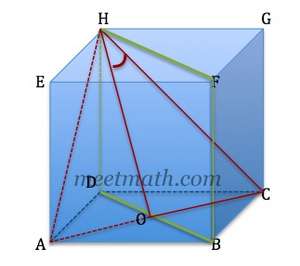
- Proyeksi CH terhadap bidang BDHF adalah garis HO (titik $O$ ditengah $AC$)
-
Sudut yang terbentuk antara garis $CH$ dengan bidang $BDHF$ adalah
-
Perhatikan $\bigtriangleup ACH$ adalah segitiga sama sisi, maka semua sudutnya $600^0$
\begin{align*}\angle CHO & = & \frac 12\angle AHC\\ & = & \frac 12.60^{\circ}\\\angle CHO & = & 30^{\circ}\\Cos\angle CHO & = & Cos\;30^{\circ}\\ & = & \frac{1}{2}\sqrt{3}\end{align*}
-
$ABCD.EFGH$ dengan panjang rusuk 6 cm. Jarak titik $A$ ke garis $CF$ adalah…
A. $6\sqrt3$ cm
B. $6\sqrt2$ cm
C. $3\sqrt6$ cm
D. $3\sqrt3$ cm
E. $3\sqrt2$ cm
Jawab :
-
Jarak titik ke garis adalah jarak dari titik tersebut terhadap titik yang merupakan perpotongan garis di atas dengan suatu garis yang tegak lurus dengan garis di atas dan memotong titik tersebut.
-
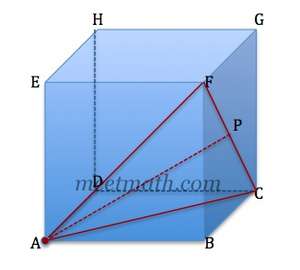
Perhatikan $\bigtriangleup ACF$ sama sisi jika rusuk kubus adalah 6 cm akan didapat :
$AF = 6\sqrt{2}$ cm
$AC = 6\sqrt{2}$ cm
$CF = 6\sqrt{2}$ cm
-
Jarak titik $A$ ke garis $CF$ kita tarik garis tegak lurus dengan garis $CF$ yang memotong titik A kita akan mendapatkan garis $AP$ ($P $ ditengah $CF$)
\begin{align*}AP & = & \sqrt{(6\sqrt{2})^{2}-(3\sqrt{2})^{2}}\\ & = & \sqrt{72-18}\\ & = & \sqrt{54}\\ & = & 3\sqrt{6} \end{align*}
-
-
Luas segi 12 beraturan dengan panjang jari-jari lingkaran luar 8 cm adalah…
A. 192 $cm^2$
B. 172 $cm^2$
C. 162 $cm^2$
D. 148 $cm^2$
E. 144 $cm^2$
Jawab :
- ingat Luas segi – n beraturan ${\color{red} L=\frac{n}{2}.r^{2}.sin\left ( \frac{2\pi}{n} \right )}$
maka :
\begin{align*}L & = & \frac{n}{2}.r^{2}.sin(\frac{2\pi}{n})\\ & = & \frac{12}{2}.8^{2}.sin(\frac{360}{12})\\ & = & 6.64.sin\;30^{0}\\ & = & 6.64.\frac{1}{2}\\ & = & 192\;\;cm^{2} \end{align*}
-
Diketahui p dan q adalah sudut lancip dan $p-q=30^0$. Jika $cos\;p.sin\;=\frac 16$, maka nilai dari$ sin p. cos p$ =…
A. $\frac 16$
B. $\frac 26$
C. $\frac 36$
D. $\frac 46$
E. $\frac 56$
Jawab :
Yang diketahui $(p-q)$ dan $cos\;p.sin\;$ maka langsung kita ingat rumus ${\color{red} sin(p-q)=sin\;p.cos\;q - cos\;p.sin\;q}$
sehingga didapat :
\begin{align*}(p-q) & = & 30^{0}\\sin\;(p-q) & = & sin\;30^{0}\\sin\;p.cos\;q-cos\;p.sin\;q & = & \frac{1}{2}\\sin\;p.cos\;q-\frac{1}{6} & = & \frac{1}{2}\\sin\;p.cos\;q & = & \frac{1}{2}+\frac{1}{6}\\sin\;p.cos\;q & = & \frac{4}{6}\end{align*}
-
Hasil dari $\Large \frac{cos(45-a)^{0}+cos(45+a)^{0}}{sin(45+a)^{0}+sin(45-a)^{0}}=$ …
A. $-\sqrt2$
B. $-1$
C. $\frac 12\sqrt2$
D. $1$
E. $\sqrt2$
Jawab :
ingat :
\begin{align*}{\color{Red} cos\;A+cos\;B=2.cos\;\frac 12(A+B).cos\;\frac 12(A-B)}\\ {\color{Red} sin\;A+sin\;B=2.sin\;\frac 12(A+B).cos\;\frac 12(A-B)} \end{align*}
maka :
\begin{align*}\frac{cos(45-a)^{0}+cos(45+a)^{0}}{sin(45+a)^{0}+sin(45-a)^{0}}\\ =\frac{2.cos\;\frac 12\left ( (45-a)+(45+a) \right ).cos\;\frac 12\left ( (45-a)-(45+a) \right )}{2.sin\;\frac 12\left ( (45+a)+(45-a) \right ).cos\;\frac 12(45+a)-(45-a)}\\=\frac{2.cos\;\frac 12.90^{\circ.}.cos\;\frac 12(-2a)}{2.sin\;\frac 12.90^{\circ}.cos\frac 12.(2a)}\\=\frac{2.cos\;45^{\circ}.cos\;a}{2.sin\;45^{\circ}.cos\;a}\\=1\end{align*}
Tunggu lagi kelanjutannya ya….tetap semangat!!!