Berikut adalah kelanjutan Pembahasan Soal Ujian Nasional SMA IPA 2010 Bagian 2.
Ingatlah selalu untuk belajar materi dasarnya yah, mari kita berlatih lagi.
-
Bentuk sederhana dari $\frac{6(3+\sqrt5)(3-\sqrt5)}{2+\sqrt6} = $…
A. $24+12\sqrt6$
B. $-24+12\sqrt6$
C. $24-12\sqrt6$
D. $-24-\sqrt6$
E. $24-12\sqrt6$
Jawab :
-
lihat pembilang, ingat selalu ${\color{Red} (a-b)(a+b)=a^{2}-b^{2}}$
-
untuk merasionalkan penyebut, kita kalikan dengan sekawan penyebutnya :
\begin{align*}\frac{6\left ( 3+\sqrt{5} \right )\left ( 3-\sqrt{5} \right )}{2+\sqrt{6}} & = & \frac{6(3^{2}-( \sqrt{5})^{2})}{2+\sqrt{6}}\;.\;\frac{2-\sqrt{6}}{2-\sqrt{6}}\\ & = & \frac{6(9-5).(2-\sqrt{6})}{2^{2}-(\sqrt{6})^{2}}\\ & = & \frac{24(2-\sqrt{6})}{4-6}\\ & = & \frac{24(2-\sqrt{6})}{-2}\\ & = & -12(2-\sqrt{6})\\ & = & -24+12\sqrt{6} \end{align*}
-
-
Suku banyak $2x^3+ax^2+bx+2$ dibagi $(x+1)$ sisanya 6 dan dibagi $(x-2) $sisanya 24. Nilai $2a – b$ = …
A. 0
B. 2
C. 3
D. 6
E. 9
Jawab :
ingat teorema sisa jika $F(x)$ dibagi $(x-h)$ maka akan bersisa $S=F(h)* F(x)=2x^{3}+ax^{2}+bx+2$
Pembagi $(x+1)$ bersisa 6 maka $h = -1$ dan $S = 6$
\begin{align*}F(h) & = S\\2(-1)^{3}+a(-1)^{2}+b(-1)+2 & = & 6\\-2+a-b+2 & = & 6\\a-b & = & 6 \end{align*}
Pembagi $(x-2)$ bersisa 24 maka $h = 2$ dan $S = 24$
\begin{align*}F(h) & = S\\2(2)^{3}+a(2)^{2}+b(2)+2 & = & 24\\16+4a+2b+2 & = & 24\\4a+2b & = & 6 \end{align*}
-
Eliminasi kedua persamaan
\begin{array}{rcl}4a+2b = 6 & [.\frac{1}{2}] & 2a+b = 3\\a-b = 6 & [.1] & \underline{\;\;a-b= 6}\;\;(+)\\ & \Leftrightarrow & 3a\;\;\;\;\;\;=9\\ & \Leftrightarrow & \;\;\;a\;\;\;\;\;=3\end{array}
-
subtitusikan ke a – b = 6
\begin{align*}a-b & = & 6\\3-b & = & 6\\b & = & -3 \end{align*}
-
-
Diketahui segitiga $PQR$ dengan $P(1, 5, 1) ; Q(3 , 4 , 1)$ dan$ R(2 , 2 , 1)$. Besar sudut $ PQR $ adalah….
A. $135^0$
B. $90^0$
C. $60^0$
D. $45^0$
E. $30^0$
Jawab :
-
Pada $\bigtriangleup PQR$, maka $\angle PQR=\angle Q$ dimana $\angle Q$ adalah sudut yang terbentuk dari $\overrightarrow{QP}$ dan $\overrightarrow{QR} $
\begin{align*}\overrightarrow{QP} & = & P-Q\\ & = & \begin{bmatrix} 1\\ 5\\ 1 \end{bmatrix}-\begin{bmatrix} 3\\ 4\\ 1 \end{bmatrix}\\\overrightarrow{QP} & = & \begin{bmatrix} -2\\ 1\\ 0 \end{bmatrix}\end{align*} dan \begin{align*}\overrightarrow{QR} & = & R-Q\\ & = & \begin{bmatrix} 2\\ 2\\ 1 \end{bmatrix}-\begin{bmatrix} 3\\ 4\\ 1 \end{bmatrix}\\\overrightarrow{QR} & = & \begin{bmatrix} -1\\ -2\\ 0 \end{bmatrix}\end{align*}
maka :
\begin{align*}cos\;\angle PQR & = & 0\\\angle PQR & = & 90^{\circ} \end{align*}
-
-
Diketahui segitiga ABC dengan koordinat $A(2, -1, -1) ; B(-1 , 4 , -2)$ dan $C (5 , 0 , -3)$. Proyeksi vektor$ \overrightarrow{AB}$ pada $\overrightarrow{AC}$ adalah..
A.$ \frac 14(3\overrightarrow{i}+\overrightarrow{j}-2\overrightarrow{k})$
B. $\frac{3}{14}(3\overrightarrow{i}+\overrightarrow{j}-2\overrightarrow{k})$
C. $-\frac 17(3\overrightarrow{i}+\overrightarrow{j}-2\overrightarrow{k})$
D. $-\frac{3}{14}(3\overrightarrow{i}+\overrightarrow{j}-2\overrightarrow{k})$
E. $-\frac{3}{7}(3\overrightarrow{i}+\overrightarrow{j}-2\overrightarrow{k})$
Jawab :
Jika Proyeksi vektor $\overrightarrow{AB}$ pada $\overrightarrow{AC}$ adalah $d$, maka ${\color{Red} d=\frac{\overrightarrow{AB}.\overrightarrow{AC}}{\left \| \overrightarrow{AC} \right \|^2}.\;\;\overrightarrow{AC}}$
-
\overrightarrow{AB}=B-A = \begin{bmatrix} -1\\ 4\\ -2 \end{bmatrix}-\begin{bmatrix} 2\\ -1\\ -1 \end{bmatrix}=\begin{bmatrix} -3\\ 5\\ -1 \end{bmatrix}
-
\overrightarrow{AC}=C-A = \begin{bmatrix} 5\\ 0\\ -3 \end{bmatrix}-\begin{bmatrix} 2\\ -1\\ -1 \end{bmatrix}=\begin{bmatrix} 3\\ 1\\ -2 \end{bmatrix}
\begin{align*}d & = & \frac{\overrightarrow{AB}.\overrightarrow{AC}}{\left \| \overrightarrow{AC} \right \|^2}.\;\;\overrightarrow{AC}\\ & = & \frac{(-3)(3)+(5)(1)+(-1)(-2)}{\left ( \sqrt{3^2+1^2+(-2)^2} \right )^2}.\;\begin{bmatrix} 3\\ 1\\ -2 \end{bmatrix}\\ & = & \frac{-2}{14}\;.\;\begin{bmatrix} 3\\ 1\\ -2 \end{bmatrix}\\ & = & -\frac{1}{7}\;\;(3\vec{i}+\vec{j}-2\vec{k})\end{align*}
-
-
Perhatikan gambar grafik fungsi eksponen!
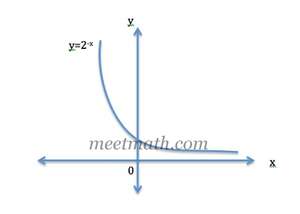
Persamaan grafik fungsi invers pada gambar adalah….
A. $y=\;^2log\;x$
B. $y=\;^{\frac 12}\;log\;x$
C. $y=\;2.\;log\;x$
D. $y=\;-2.\;log\;x$
E. $y=-\frac 12.\;log\;x$
Jawab :
ingat notasi logaritma $a^{x}=y\Leftrightarrow ^{a}log\;y=x$
maka :
\begin{align*}y=2^{-x} & \Leftrightarrow & ^{2}log\;y=-x\\ & \Leftrightarrow & -^{2}log\;y=x\\ & \Leftrightarrow & (\frac{1}{-1}).^{2}log\;y=x\\ & \Leftrightarrow & ^{2^{-1}}log\;y^{1}=x\\ & \Leftrightarrow & ^{\frac{1}{2}}log\;y=x \end{align*}
Sehingga invers fungsi adalah $ y=\;^{\frac{1}{2}}log\;x$
ok…. tunggu soal selanjutnya