Dalam geometri, Titik disimbolkan dengan noktah dimana titik itu sendiri tidak mempunyai ukuran,tidak mempunyai panjang maupun luas apalagi volume
Garis merupakan himpunan titik-titik yang mempunyai ukuran panjang
Sedangkan Bidang merupakan himpunan garis-garis yang mempunyai ukuran panjang dan lebar
A. Kedudukan Titik, Garis, dan Bidang
1. Kedudukan Titik Terhadap Garis
a. Titik terletak Pada Garis, dapat diartikan juga bahwa, garis melalui titik tersebut.

b. Titik terletak di Luar Garis, dapat diartikan juga bahwa, garis tidak melalui titik tersebut

2. Kedudukan Titik Terhadap Bidang
a. Titik terletak pada Bidang, dapat diartikan juga bahwa, bidang melalui titik tersebut.
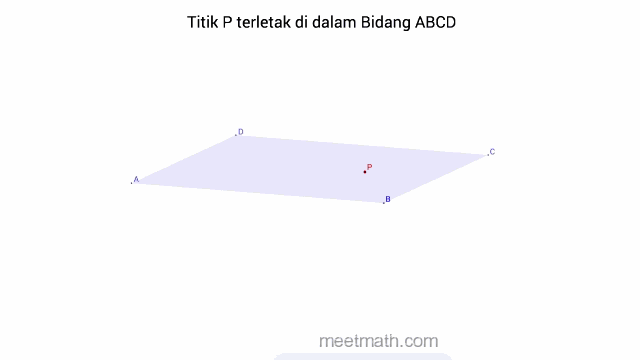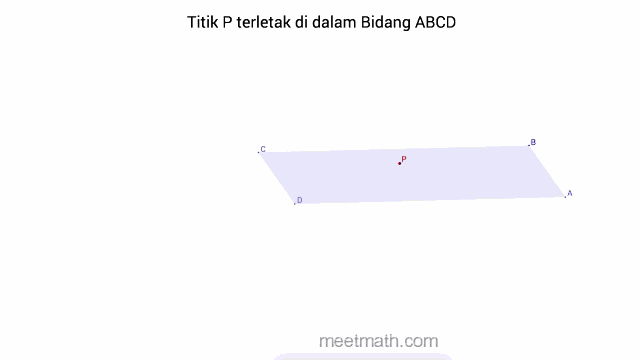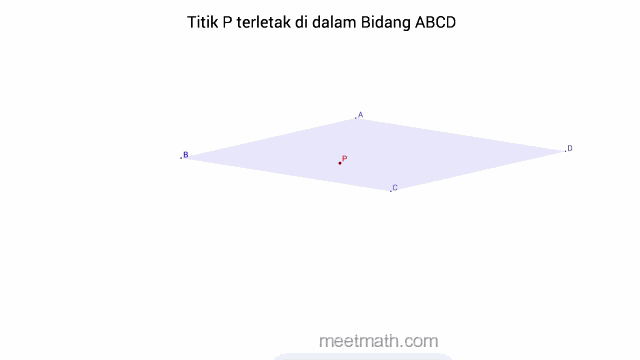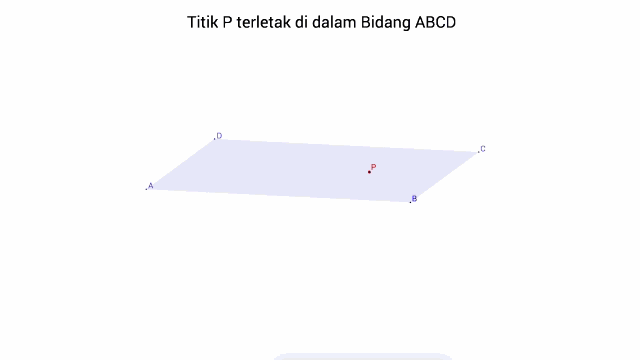
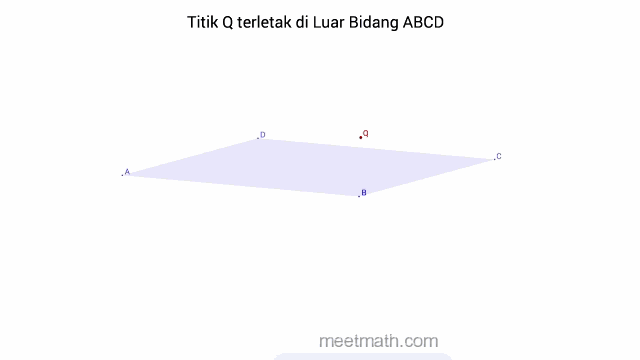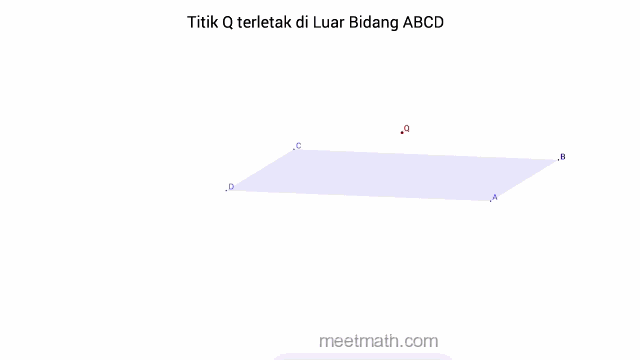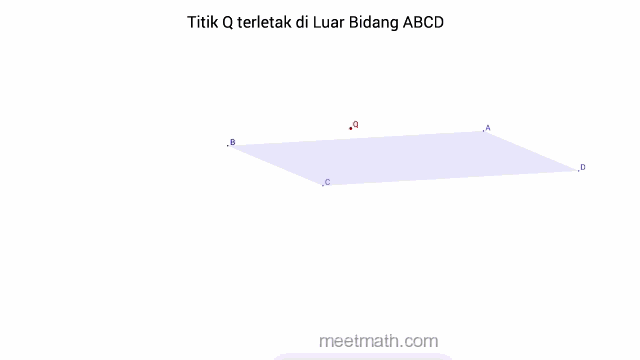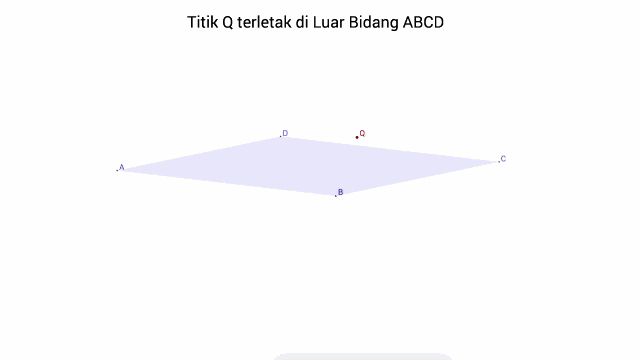
b. Titik terletak di Luar Bidang
dapat diartikan juga bahwa, bidang sama sekali tidak melalui titik tersebut.
3. Kedudukan Garis Terhadap Garis
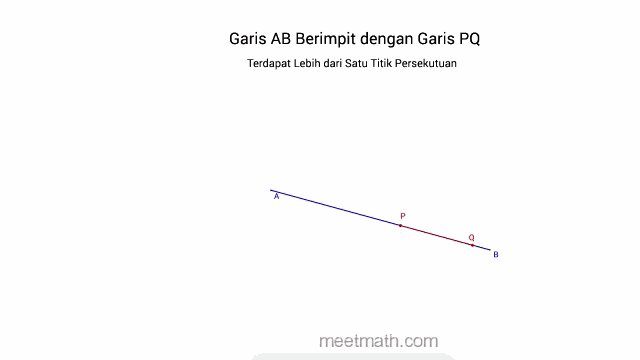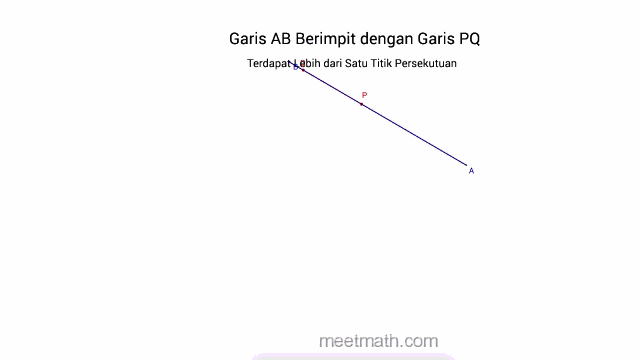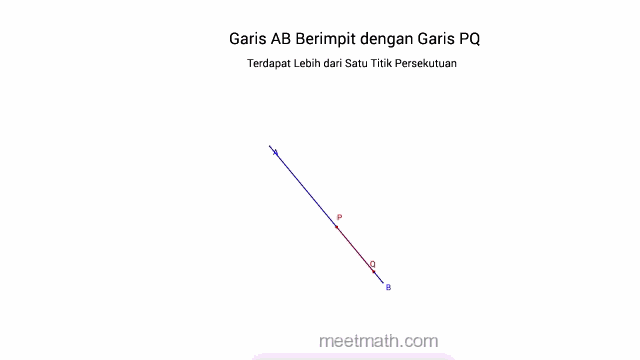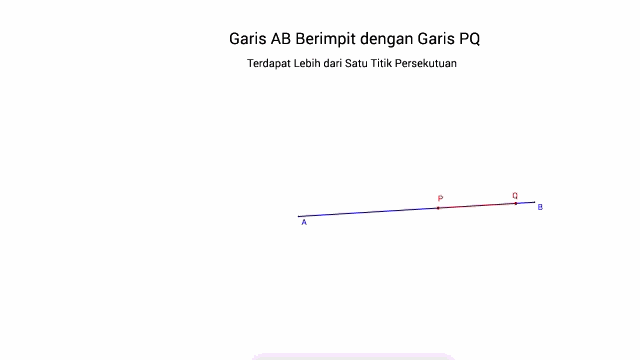
a. Dua Garis saling Berhimpit jika terdapat lebih dari satu titik persekutuan (titik potong)
b. Dua Garis saling Berpotongan jika terdapat tepat satu titik persekutuan (titik potong)

c. Dua Garis saling Sejajar jika tidak ada satupun titik persekutuan

d. Dua Garis saling Bersilangan jika tidak saling Berpotongan, tidak saling Sejajar dan tidak terletak pada satu bidang
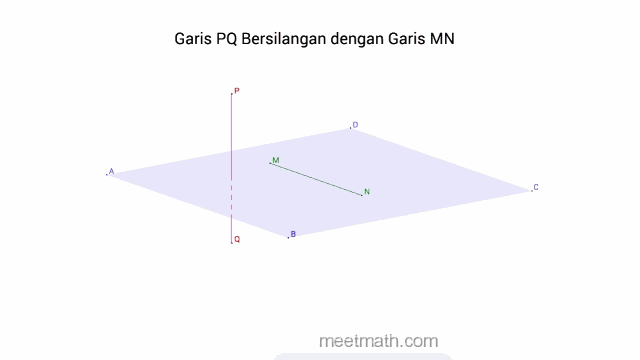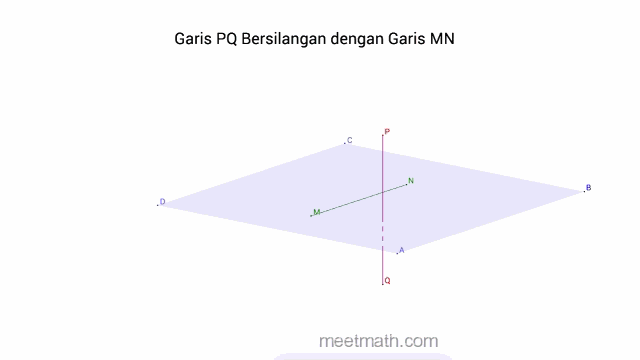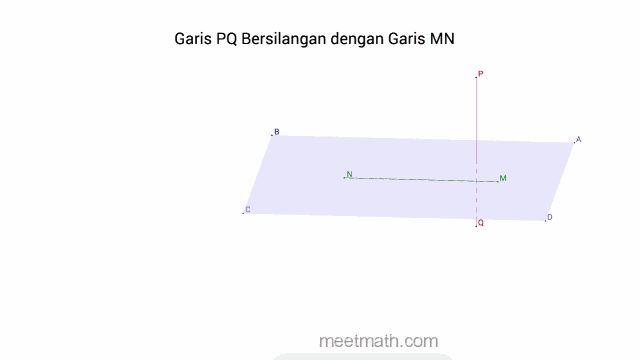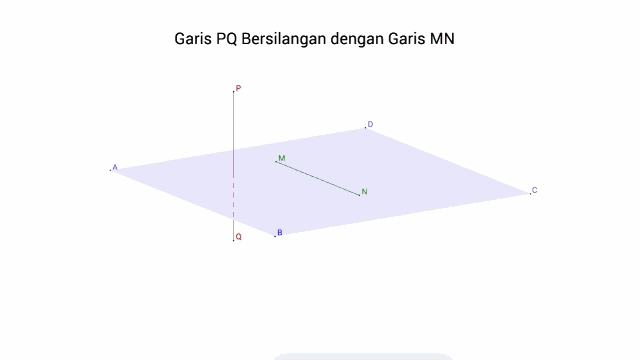
4. Kedudukan Garis Terhadap Bidang
a. Garis Terletak pada Bidang jika terdapat lebih dari satu titik persekutuan
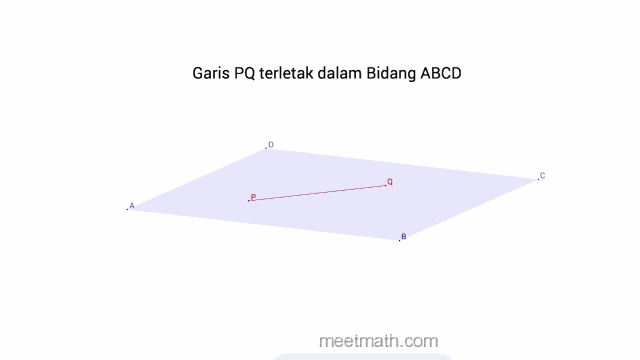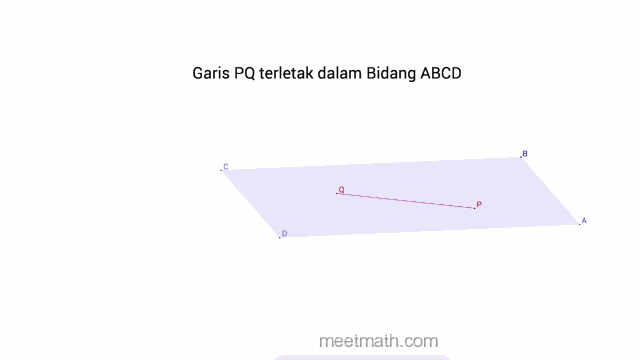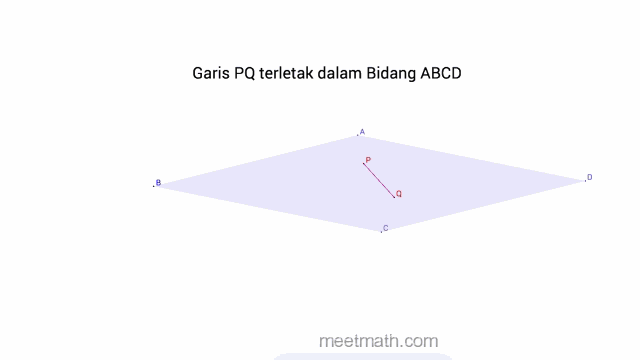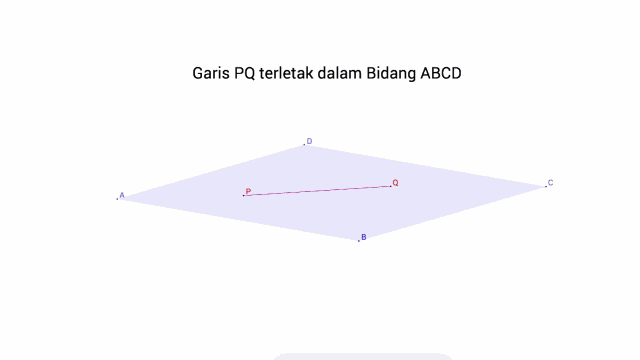
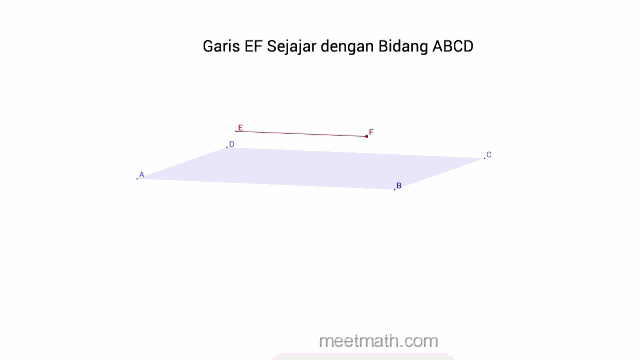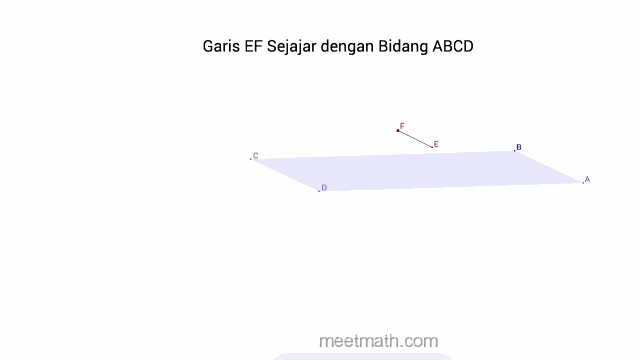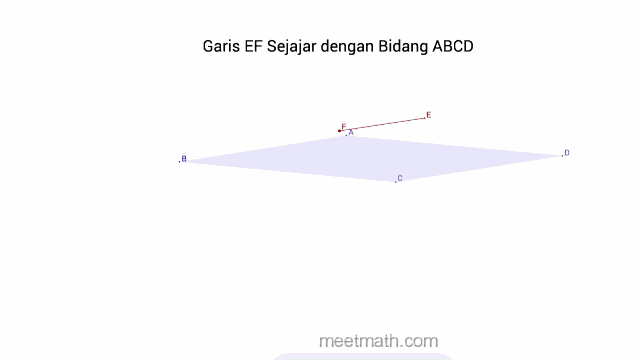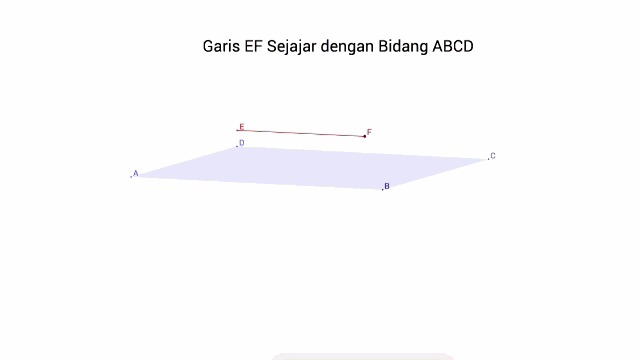
b. Garis Sejajar pada Bidang jika sama sekali tidak terdapat titik persekutuan
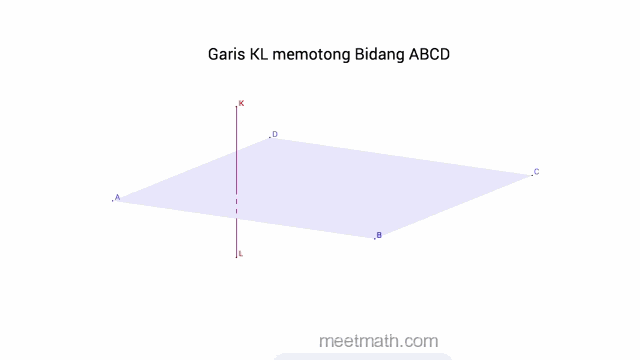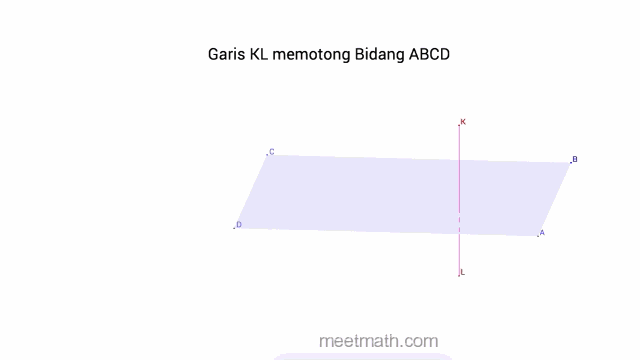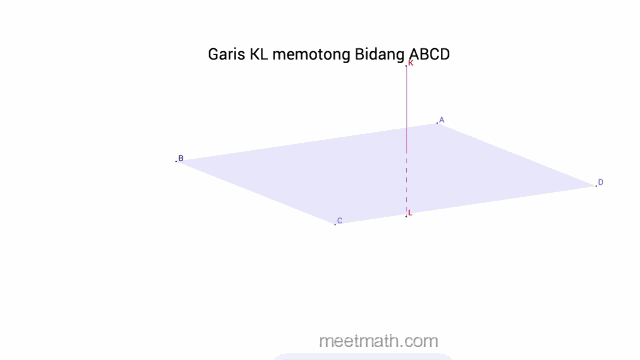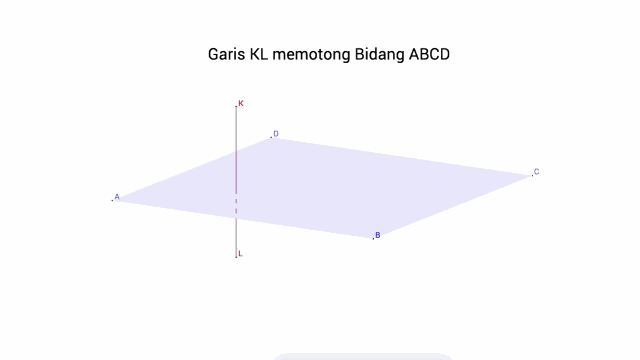
c. Garis Berpotongan pada Bidang jika terdapat tepat satu titik persekutuan (titik tembus)
5. Kedudukan Bidang terhadap Bidang
a. Dua Bidang saling Berimpit, jika setiap titik di satu Bidang, juga terletak pada Bidang lainya
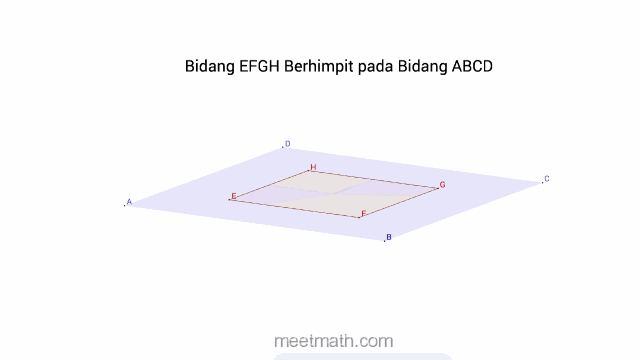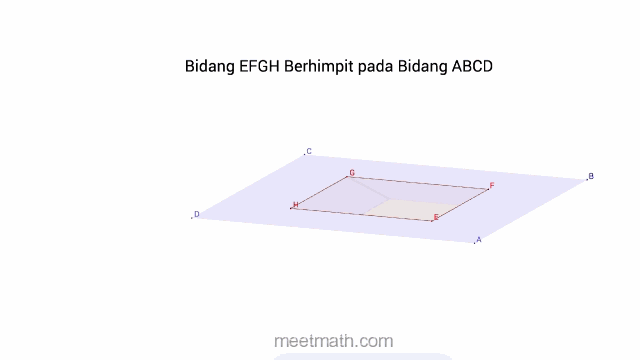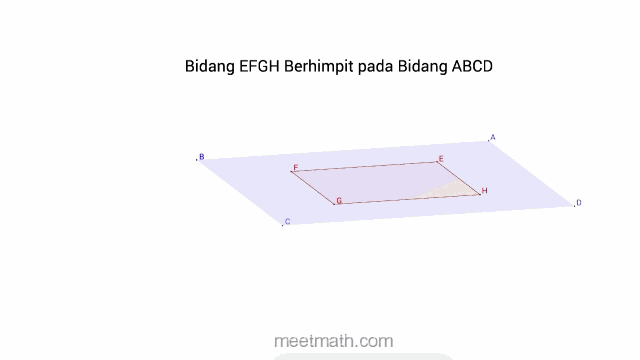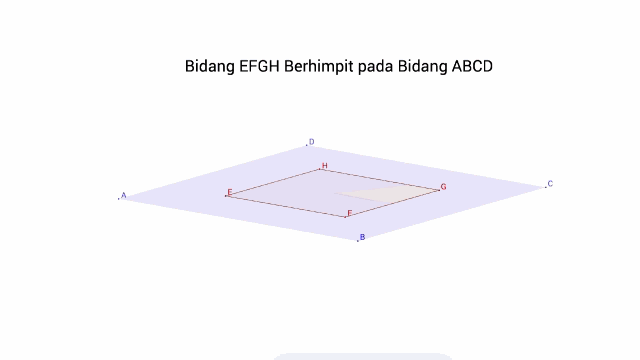
b. Dua Bidang saling Sejajar, jika tidak ditemukan satupun titik persekutuan

c. Dua Bidang saling Berpotongan, jika terdapat tepat satu garis persekutuan
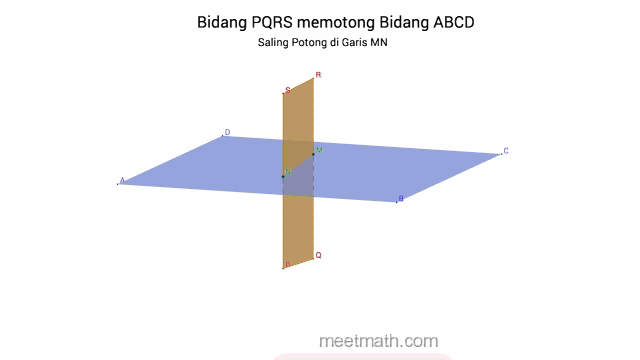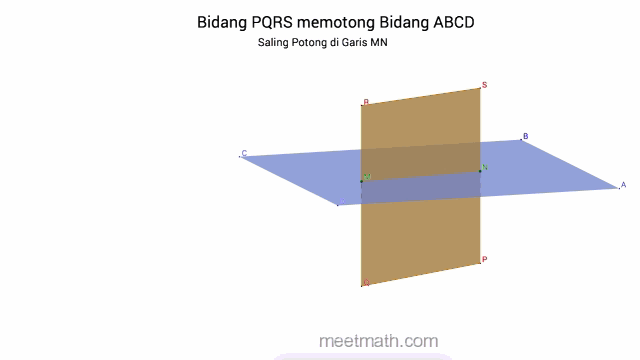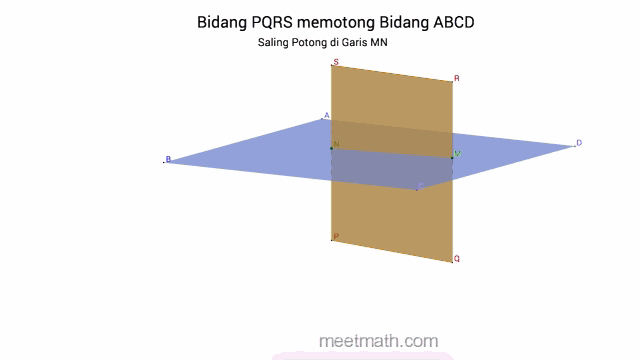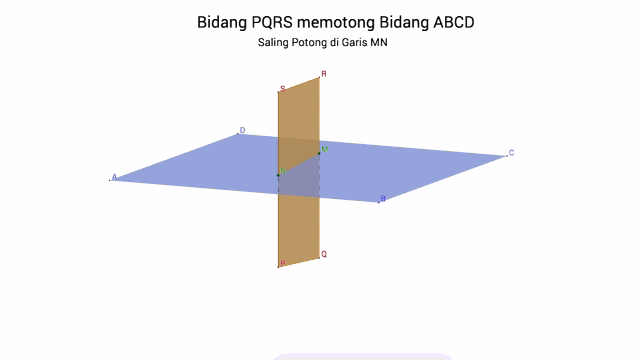
B. Titik, Garis dan Bidang pada Kubus
Perhatikan Kubus ABCD.EFGH di bawah ini :
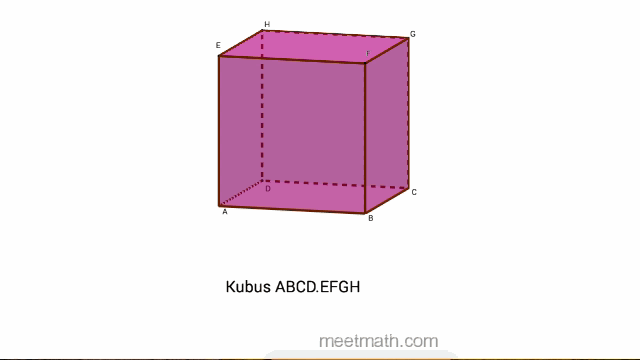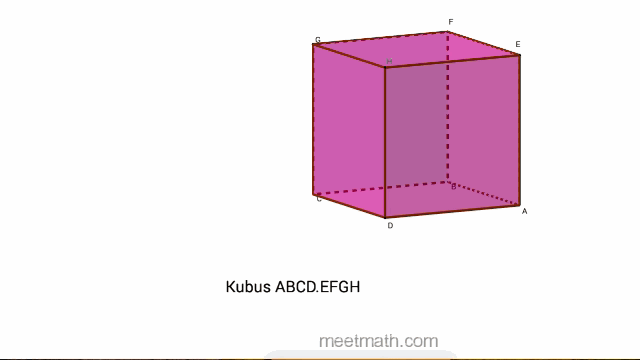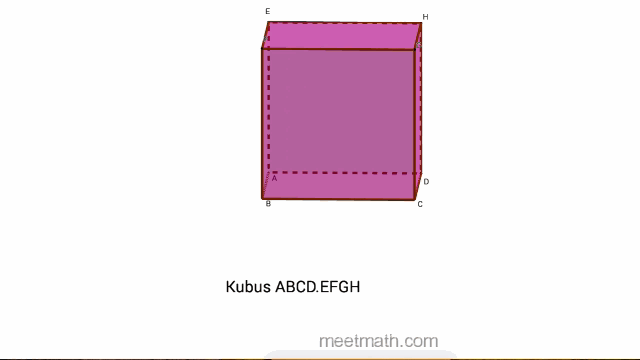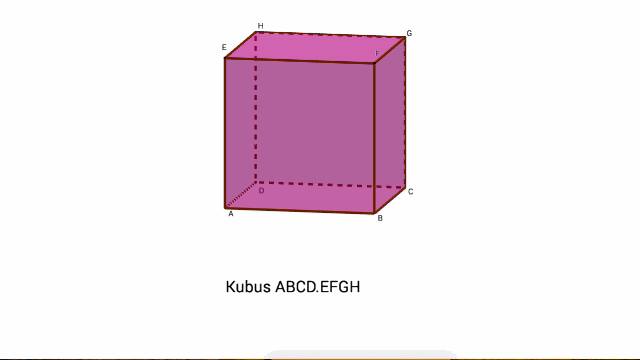
A adalah sebuah Titik pada kubus ABCD.EFGH
AB adalah sebuah Garis pada kubus ABCD.EFGH disebut juga rusuk kubus
ABCD adalah sebuah Bidang pada kubus ABCD.EFGH disebut juga Bidang sisi kubus
Sekarang kita perhatikan contoh kedudukan Titik, Garis dan Bidang pada kubus ABCD.EFGH berikut :
1. Kedudukan Titik A dan garis AB = Titik A berada dalam garis AB
2. Kedudukan Titik E dan garis GH = Titik E berada di luar garis GH
3. Kedudukan Titik B dan Bidang ABCD = Titik B berada di dalam Bidang ABCD
4. Kedudukan Titik G dan Bidang ABFE = Titik G berada di luar bidang ABFE
5. Kedudukan garis AD dan garis FG = Garis AD sejajar garis FG
6. Kedudukan Garis DH dan Garis GH = Garis DH Berpotongan dengan garis GH (yaitu di titik H) lebih tepatnya Garis DH Saling Tegak Lurus dengan garis GH
7. Kedudukan Garis AC dan Bidang ABCD = Garis AC Berpotongan dengan bidang ABCD di titik C
8. Kedudukan Garis AB dan garis CG = Garis AB Bersilangan dengan garis CG
9. Kedudukan Bidang ABCD dan Bidang EFGH = Bidang ABCD sejajar bidang EFGH
10. Kedudukan Bidang BDHF dan bidang ABFE = Bidang BDHF Berpotongan dengan bidang ABFE di garis BF