Dimensi Tiga Kubus

Materi Dimensi Tiga mencakup tentang jarak, sudut pada bangun ruang.

Untuk itulah kita wajib tau tiap bangun ruang . Target kita yang pertama adalah Kubus . Pasti dengar namanya saja udah bisa membayangkan bentuknya kan ?

Nah, mari kita kupas tentang sifat-sifat si Kubus ini !

KUBUS ABCD.EFGH

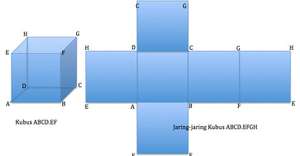
Dalam kubus ABCD.EFGH terdapat :

12 rusuk contoh AB 12 diagonal sisi / diagonal bidang contoh EG 6 bidang / sisi contoh CDHG 6 bidang diagonal contoh ACGE 4 diagonal ruang contoh AG

Yuuuk kita cari rumus diagonal sisi dan diagonal ruang pada kubus ABCD.EFGH dulu yuuuuuuuuuk….

• kita akan cari diagonal sisi AC, perhatikan bidang ABCD (persegi)

  

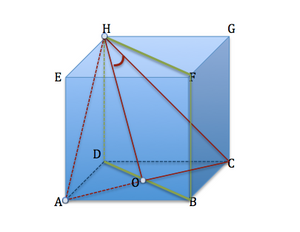
  \begin{align}AC&=&\sqrt{AB^2+BC^2}\\&=&\sqrt{r^2+r^2}\\&=&\sqrt{2r^2}\\&=&r\sqrt 2\end{align}

• kita akan cari diagonal ruang AG, perhatikan bidang diagonal ACGE (persegi panjang)
  

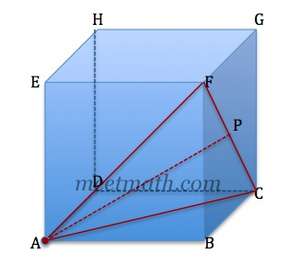
  \begin{align}AG&=&\sqrt{AC^2+CG^2}\\&=&\sqrt{(r\sqrt 2)^2+r^2}\\&=&\sqrt{2r^2+r^2}\\&=&\sqrt{3r^2}\\&=&r\sqrt 3\end{align}

Kita rangkum Rumus Kubus dengan rusuk = r

• diagonal sisi kubus = $r\sqrt 2$
• diagonal ruang kubus = $r\sqrt 3$
• Luas permukaan kubus = $6.r^2$
• Volume kubus = $r^3$

Contoh soal :

1. Jika diketahui kubus dengan diagonal sisinya $2\sqrt 6$ cm , tentukan diagonal ruang kubus !

   jawab :

   pertama kita cari rusuk nya dulu ya,

   \begin{align*}diagonal.sisi&=&2\sqrt 6\\r\sqrt 2&=&2\sqrt 6\\r&=&\frac{2\sqrt 6}{\sqrt 2}\\r&=&2\sqrt 3 \end{align*} 

   maka diagonal ruang kubus :

   \begin{align*}diagonal.ruang&=&{\color{Red} r}\sqrt 3\\&=&({\color{Red} 2\sqrt 3})\sqrt 3\\&=&2.3\\&=&6 \end{align*}
    

2. Jika diketahui kubus ABCD.EFGH dengan rusuk 5 cm, tentukan luas BDHF !

   jawab :

   perhatikan BDHF (bidang diagonal) dengan BF = 5 cm (rusuk) dan BD = $5\sqrt 2$ cm (diagonal sisi)

   maka luas BDHF

   \begin{align*}L_{BDHF}&=&BD\times BF\\&=&5\sqrt 2\times 5\\&=&25\sqrt 2\;\;cm^2\end{align*} 

3. Jika diketahui kubus dengan diagonal sisi 6 cm, tentukan Volume kubus tersebut !

   jawab :

   pertama kita cari rusuknya ya.. 

   \begin{align*}diagonal.sisi&=&6\\r\sqrt 2&=&6\\r&=&\frac{6}{\sqrt 2}.\frac{\sqrt 2}{\sqrt 2}\\&=&\frac{6}{2}\sqrt 2\\r&=&3\sqrt 2\end{align*}

   maka volume kubus :

   \begin{align*}V&=&r^3\\&=&(3\sqrt 2)^3\\&=&27.2\sqrt 2\\&=&54\sqrt 2\;\;cm^3\end{align*}

Sekarang kita masuk ke contoh soal yang berkaitan dengan jarak dan sudut pada bangun ruang…..yuk

Latihan soal bangun ruang yang berkaitan dengan jarak dan sudut

1. Pada kubus ABCD.EFGH dengan rusuk 4 cm, tentukan jarak titik B ke garis EG !

   jawab :

   

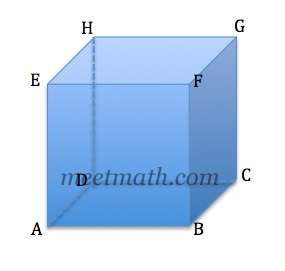
   titik B dan garis EG berada dalam satu bidang yaitu segitiga BEG(sama sisi) perhatikan bahwa BE , BG dan EG adalah diagonal sisi sehingga BE = BG = EG = $4\sqrt 2$ cm

   proyeksi titik B di garis EG adalah titik P (di tengah EG) sehingga GP = $2\sqrt 2$ cm

   jarak yang akan kita cari adalah panjang garis BP

   maka :

2. Pada kubus ABCD.EFGH tentukan jarak titik A ke garis CE !

   jawab :

   

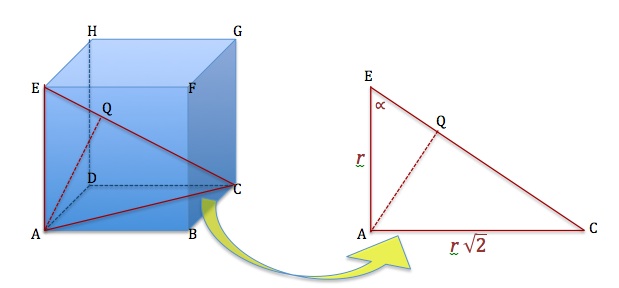
   • titik A dan garis EC berada dalam satu bidang yaitu segitiga AEC
   • perhatikan bahwa AE adalah rusuk, kita misalkan $AE = r$ , sedangkan AC adalah diagonal sisi maka kita misalkan $AC = r\sqrt 2$
   • proyeksi titik A di garis EC adalah titik Q ( AQ tegak lurus EC)
   • jarak yang akan kita cari adalah panjang garis AQ

   perhatikan segitiga AQE dan segitiga CAE kita gunakan perbandingan sisi